Generating virtual mazes

An important part of umaze is generating a maze inside an area specified by the user on a map. A simple approach for reaching this goal is to start by generating a grid inside this area, consisting of all possible walls in logical places inside the area, and then removing some of those walls to open passages inside the maze. Let’s look at the problem in pieces.

Defining the grid

First we need to decide how dense the grid shall be. For a walking maze corridors of about one meter in width would be sufficient. For umaze they have to be wider, though, because the accuracy of GNSS on typical smart phones is not quite yet in the sub-meter range.

As an interesting tidbit for the implementation of map-using applications, an early definition of one meter defined it so that the shortest distance from the North Pole to the equator would be 10000 km, when passing via Paris. Going around the whole Earth would thus take 40000 km. (see e.g. https://en.wikipedia.org/wiki/History_of_the_metre)

With this value (new measurements have changed it slightly) it is possible to get the length of one degree of latitude (north-south direction) as 10000 km / 90 degrees = 111.1 kilometers. Conversely 1 meter, a rather handy distance in daily life, is about 90 degrees / 10000000 m = 0.000009 degrees/m.

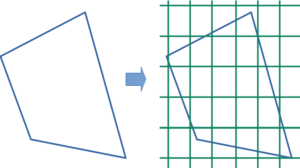
Once we know the distance between lines in the grid, next we should decide how to align it on the shape we want to cover. In the case of rectangles and other regular shapes the choice might be obvious (to a human). Generally, however, the shape may not be regular, and around the edges the cells in the grid can be cut by the boundary of the shape. In umaze the incomplete cells are merged with their neighbor cells in order to ensure that all parts of the maze are large enough for walking through, should there be a passage in that part.

Making a maze inside the grid

For our purposes making a maze inside the grid means removing just enough walls from the grid so that any cell can be reached from any other cell in the grid. There are plenty of algorithms for this. A good listing with examples is given at http://weblog.jamisbuck.org/2011/2/7/maze-generation-algorithm-recap. In umaze we use currently a version based on Kruskal’s algorithm. In brief, the algorithm looks at all the walls in the grid in a random order, removing a wall and thus connecting two neighbor cells only if there is no other connection between those cells through some previously removed walls.

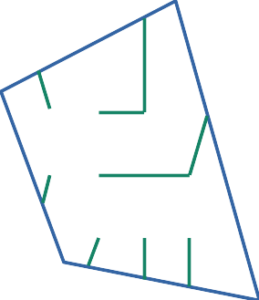
Below is a simple maze inside the previous example polygon. This maze is obviously missing entrances and perhaps challenge as well. The latter can be fixed by changing either the polygon size, the grid spacing, or perhaps the maze generation algorithm. The former will be discussed in a future blog post.